All the geometric properties of a ship as a function of mean draft have been computed and put into a single graph for convenience. This graph is called the “curves of form”. Each ship has unique curves of form. There are also tables with the same information which are called the tabular curves of form.
It is difficult to fit all the different properties on a single sheet because they vary so greatly in magnitude. To fit all the curves on a single sheet of paper one of two things must be done.
One: Provide a series of different scales on the “x” axis so that each property has its own “x” axis scale.
Two: Plot each characteristic against a common scale on the “x” axis and use a scaling factor to bring the curves numerically closer.
Using the second method requires you to read a value off the common scale and then multiply that value by the curves scale factor to obtain the real value. Each scale factor also has units associated with it. Don’t forget to do this extra step!
There are curves of form for common navy ships in the back of this text under the “Ship’s Data” section. For convenience the curves of form for the Naval Academy’s Yard Patrol Craft has been provided at Figure 4 of Annex-1 as well as in the back in the “Ship’s Data” section.
The curves of form assume that the ship is floating on an even keel (i.e. zero list and zero trim). If the ship has a list or trim then the ship’s mean draft should be use when entering the curves of form.
Keep in mind that all properties on the “curves of form” are functions of mean draft and geometry. When weight is added, removed, or shifted, the operating waterplane and submerged volume change form so that all the geometric properties also change.
In typical calculations only small draft changes occur so that the properties in the curves of form also only undergo small changes. This means for most problems it doesn't matter if you look up the properties at the initial mean draft, final mean draft, or average mean draft. Numerically they all will be very close and shouldn't affect your final answer. If the draft changes by an amount that causes large changes in the properties, then an average draft of the initial and final drafts should be used.
The following is a list of each characteristic found on the “curves of form” with a brief explanation of its meaning.
Other disciplines of science also use the word ton as follows. A long ton (LT) is the same as the ton equal to 2240 lb. A short ton (ST) is equal to 2000 lb . A metric ton (Tonne) is equal to 1000 kg. In this course “ton” will always mean 2240 lb.
To obtain just parallel sinkage the weight added would need to be “effectively” added to the center of flotation because the center of flotation is the pivot point of the ship while it is floating. The units on TPI are long tons per inch. If an equivalent weight is removed than you lose one inch of parallel sinkage. You will be using TPI in chapter 3 when you do trim problems.
An approximate formula for TPI based on the area of the waterplane can be derived as follows:
Note 1: Archimedes equation has been used to convert weight to the product of volume, density, and the magnitude of the acceleration of gravity.
Note 2: TPI is defined for a ship in salt water at 59 degrees Fahrenheit which allows the use of 1.99 lb s2 / ft4 for the density.
Note 3: It is assumed that the waterplane area doesn’t change much in one inch so that the volume required for one inch of submergence can be approximated by the product of the waterplane area and 1 inch of thickness. This is the same as assuming the volume is a right prism with the waterplane as the cross section and a height of one inch.
To calculate the change in draft due to parallel sinkage the following equation is used:
WPA or Awp stands for the waterplane area. The units of WPA are ft2. This waterplane area can be calculated with Simpson’s rule.
LCF is the longitudinal center of flotation. It is the distance in feet from the longitudinal reference to the center of flotation. The reference position could be the FP or midships. If it is midships remember that distances aft of midships are negative. The LCF can be calculated using table of offsets and Simpson’s rule.
Trim is defined as the draft aft minus the draft forward.
By convention when a ship is down by the bow it is assigned a negative trim.
To compute the change in trim due to a weight shift or addition the following equation is used:
This stands for the distance in feet from the keel to the longitudinal metacenter. For now just assume the metacenter is a convenient reference point vertically above the keel of the ship for Naval Architecture calculations. This distance is on the order of one hundred to one thousand feet whereas the distance from the keel to the transverse metacenter is only on the order of ten to thirty feet.
You have done the calculations for at least two of the properties listed in the curves of form. This should have given you an appreciation for how the curves of form are constructed. Given more time and a little more instruction you could use a table of offsets and numerical integration to obtain the rest of the properties. Be grateful that all these calculations have been done already so that all you have to do is look up these values.
Be sure that, given a ship’s curves of form and a mean draft, you can find any of the properties listed above. You will need this skill to obtain the values for calculations that will follow in subsequent chapters.
It is difficult to fit all the different properties on a single sheet because they vary so greatly in magnitude. To fit all the curves on a single sheet of paper one of two things must be done.
One: Provide a series of different scales on the “x” axis so that each property has its own “x” axis scale.
Two: Plot each characteristic against a common scale on the “x” axis and use a scaling factor to bring the curves numerically closer.
Using the second method requires you to read a value off the common scale and then multiply that value by the curves scale factor to obtain the real value. Each scale factor also has units associated with it. Don’t forget to do this extra step!
There are curves of form for common navy ships in the back of this text under the “Ship’s Data” section. For convenience the curves of form for the Naval Academy’s Yard Patrol Craft has been provided at Figure 4 of Annex-1 as well as in the back in the “Ship’s Data” section.
The curves of form assume that the ship is floating on an even keel (i.e. zero list and zero trim). If the ship has a list or trim then the ship’s mean draft should be use when entering the curves of form.
Keep in mind that all properties on the “curves of form” are functions of mean draft and geometry. When weight is added, removed, or shifted, the operating waterplane and submerged volume change form so that all the geometric properties also change.
In typical calculations only small draft changes occur so that the properties in the curves of form also only undergo small changes. This means for most problems it doesn't matter if you look up the properties at the initial mean draft, final mean draft, or average mean draft. Numerically they all will be very close and shouldn't affect your final answer. If the draft changes by an amount that causes large changes in the properties, then an average draft of the initial and final drafts should be used.
Curve of Form Definitions
The following is a list of each characteristic found on the “curves of form” with a brief explanation of its meaning.
Displacement (Δ)
This is the weight of the water displaced by the ship for a given draft assuming the ship is in salt water with a density of 1.99 lb s2 / ft4. For a freely floating ship in salt water this is numerically equal to the weight of the ship. The typical unit on displacement for Naval Ships is the long ton. One long ton (LT) equals 2240 lb.Other disciplines of science also use the word ton as follows. A long ton (LT) is the same as the ton equal to 2240 lb. A short ton (ST) is equal to 2000 lb . A metric ton (Tonne) is equal to 1000 kg. In this course “ton” will always mean 2240 lb.
LCB
This is the longitudinal center of buoyancy. It is the distance in feet from the longitudinal reference position to the center of buoyancy. The reference position could be the FP or midships. If it is midships remember that distances aft of midships are negative.VCB
This is the vertical center of buoyancy. It is the distance in feet from the baseplane to the center of buoyancy. Sometimes this distance is labeled KB with a bar over the letters.Immersion or TPI
TPI stands for tons per inch immersion or sometimes just called immersion. It is just what the words say it is. TPI is defined as the tons required to obtain one inch of parallel sinkage in salt water. Parallel sinkage is when the ship changes it’s forward and after drafts by the same amount so that no change in trim occurs.To obtain just parallel sinkage the weight added would need to be “effectively” added to the center of flotation because the center of flotation is the pivot point of the ship while it is floating. The units on TPI are long tons per inch. If an equivalent weight is removed than you lose one inch of parallel sinkage. You will be using TPI in chapter 3 when you do trim problems.
An approximate formula for TPI based on the area of the waterplane can be derived as follows:
Note 1: Archimedes equation has been used to convert weight to the product of volume, density, and the magnitude of the acceleration of gravity.
Note 2: TPI is defined for a ship in salt water at 59 degrees Fahrenheit which allows the use of 1.99 lb s2 / ft4 for the density.
Note 3: It is assumed that the waterplane area doesn’t change much in one inch so that the volume required for one inch of submergence can be approximated by the product of the waterplane area and 1 inch of thickness. This is the same as assuming the volume is a right prism with the waterplane as the cross section and a height of one inch.
To calculate the change in draft due to parallel sinkage the following equation is used:
WPA or Awp
WPA or Awp stands for the waterplane area. The units of WPA are ft2. This waterplane area can be calculated with Simpson’s rule.
LCF
LCF is the longitudinal center of flotation. It is the distance in feet from the longitudinal reference to the center of flotation. The reference position could be the FP or midships. If it is midships remember that distances aft of midships are negative. The LCF can be calculated using table of offsets and Simpson’s rule.
Moment/ Trim 1" or MT1"
This stands for the moment to change trim one inch. The units are LT-ft per inch. The ship will rotate about the center of flotation when a moment is applied to it. The moment can be produced by adding, removing, or shifting a weight some distance from the center of flotation. There are an infinite number of possible combinations of weights and distances to achieve the moment.Trim is defined as the draft aft minus the draft forward.
By convention when a ship is down by the bow it is assigned a negative trim.
To compute the change in trim due to a weight shift or addition the following equation is used:
KML
This stands for the distance in feet from the keel to the longitudinal metacenter. For now just assume the metacenter is a convenient reference point vertically above the keel of the ship for Naval Architecture calculations. This distance is on the order of one hundred to one thousand feet whereas the distance from the keel to the transverse metacenter is only on the order of ten to thirty feet.
KMT
This stands for the distance in feet from the keel to the transverse metacenter. Typically, Naval Architects do not bother putting the subscript “T” for any property in the transverse direction because it is assumed that when no subscript is present the transverse direction is implied.You have done the calculations for at least two of the properties listed in the curves of form. This should have given you an appreciation for how the curves of form are constructed. Given more time and a little more instruction you could use a table of offsets and numerical integration to obtain the rest of the properties. Be grateful that all these calculations have been done already so that all you have to do is look up these values.
Be sure that, given a ship’s curves of form and a mean draft, you can find any of the properties listed above. You will need this skill to obtain the values for calculations that will follow in subsequent chapters.
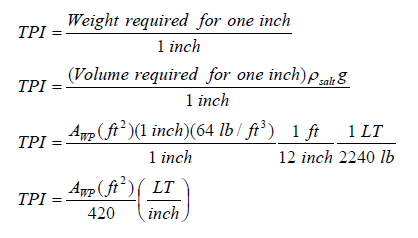


No comments:
Post a Comment